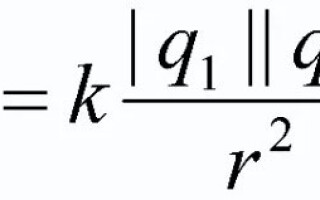Coulomb yasası, tanımı ve formülü - elektrik nokta yükleri ve etkileşimleri

Yüklü cisimler arasında birbirlerini çekebilecekleri veya itebilecekleri bir etkileşim kuvveti vardır. Coulomb yasası bu kuvveti tanımlar, vücudun büyüklüğüne ve şekline bağlı olarak etkisinin derecesini gösterir. Bu fiziksel yasa bu makalede tartışılacaktır.

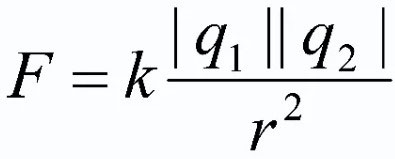
Coulomb yasası formülü.

İçerik

1 Sabit nokta ücretleri
2 Charles Coulomb'un burulma dengesi
3 Orantılılık faktörü k ve elektrik sabiti
4 Coulomb kuvvetinin yönü ve formülün vektör formu
5 Coulomb yasasının pratikte uygulandığı yerler
6 Coulomb yasasında kuvvetlerin yönü
7 Yasanın keşfinin tarihi

Sabit nokta ücretleri

Coulomb yasası, diğer nesnelerden uzaklıklarından çok daha küçük olan sabit cisimler için geçerlidir. Bir nokta elektrik yükü bu tür cisimler üzerinde yoğunlaşmıştır. Fiziksel problemleri çözerken, dikkate alınan cisimlerin boyutları ihmal edilir, çünkü gerçekten önemli değiller.

Pratikte, hareketsiz durumdaki nokta yükler aşağıdaki gibi gösterilir:

Nokta pozitif yüklü yük q1. Nokta pozitif yüklü yük q2.

Bu durumda q₁ ve q₂ - bu pozitif elektrik yükleri ve Coulomb kuvveti onlara etki eder (şekilde gösterilmemiştir). Nokta özelliklerinin boyutu önemli değildir.

Not! Dinlenme halindeki yükler, problemlerde genellikle r harfi ile gösterilen, birbirinden belirli bir mesafede bulunur. Makalede ayrıca, bu suçlamalar bir boşlukta ele alınacaktır.

Charles Coulomb'un burulma dengesi

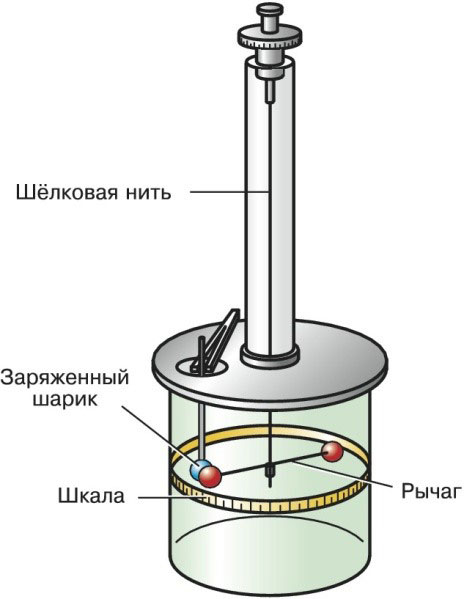
Coulomb tarafından 1777'de geliştirilen bu cihaz, daha sonra kendi adıyla anılacak olan kuvvetin bağımlılığını ortaya çıkarmaya yardımcı oldu. Yardımı ile nokta yüklerin ve ayrıca manyetik kutupların etkileşimi incelenir.

Bir burulma terazisi, dengeli bir kolun asılı olduğu dikey bir düzlemde bulunan küçük bir ipek ipliğe sahiptir. Nokta yükler, kolun uçlarında bulunur.

Dış kuvvetlerin etkisi altında, kol yatay olarak hareket etmeye başlar. Kol, ipliğin elastik kuvveti ile dengelenene kadar düzlemde hareket edecektir.

Hareket sürecinde, kol dikey eksenden belirli bir açıyla sapar. d olarak alınır ve dönme açısı olarak adlandırılır. Bu parametrenin değeri bilindiğinde ortaya çıkan kuvvetlerin torkunu bulmak mümkündür.

Ayrıca okuyun: Basit kelimelerle elektrik akımı nedir

Charles Coulomb'un burulma dengesi şöyle görünür:

Charles Coulomb'un burulma dengesi.

Orantılılık faktörü k ve elektrik sabiti 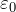$\varepsilon_0$

Coulomb yasasının formülünde k parametreleri vardır - orantılılık katsayısı veya $\varepsilon_0$ elektrik sabitidir. elektrik sabiti $\varepsilon_0$ birçok referans kitabında, ders kitabında, internette sunulmuştur ve sayılmasına gerek yoktur! Vakum orantılılık faktörü $\varepsilon_0$ iyi bilinen formülle bulunabilir:

$k = \frac {1}{4\cdot \pi\cdot \varepsilon_0}$

Burada $\varepsilon_0=8.85\cdot 10^{-12} \frac {C^2}{H\cdot m^2}$ elektrik sabitidir,

$\pi=3.14$ - Pi,

$k=9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ vakumda orantı katsayısıdır.

Ek Bilgiler! Yukarıda sunulan parametreleri bilmeden, iki nokta elektrik yükü arasındaki etkileşim kuvvetini bulmak işe yaramaz.
Coulomb yasasının formülasyonu ve formülü

Yukarıdakileri özetlemek için, elektrostatik ana yasasının resmi formülasyonunu vermek gerekir. Şu şekli alır:

Durgun haldeki iki noktasal yükün boşlukta etkileşim kuvveti, bu yüklerin çarpımı ile doğru orantılı ve aralarındaki uzaklığın karesi ile ters orantılıdır. Üstelik ücretlerin ürünü modulo alınmalı!

$F=k\cdot \frac {|q_1|\cdot |q_2|}{r^2}$

Bu formülde q₁ ve q₂nokta yükler, kabul edilen cisimler; r² - karede alınan bu cisimler arasındaki düzlemdeki mesafe; k orantılılık katsayısıdır ( $9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ vakum için).

Coulomb kuvvetinin yönü ve formülün vektör formu

Formülün tam olarak anlaşılması için Coulomb yasası görselleştirilebilir:

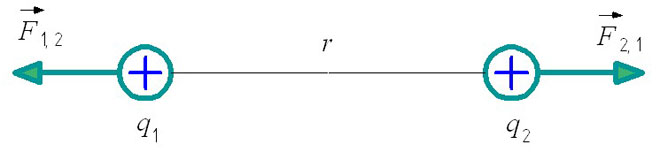
Aynı polariteye sahip iki nokta yükü için Coulomb kuvvetinin yönü.

F_1,2- birinci yükün ikinciye göre etkileşim gücü.

F_2,1- ikinci yükün birincisine göre etkileşim gücü.

Ayrıca, elektrostatik problemlerini çözerken, önemli bir kuralı dikkate almak gerekir: aynı adı taşıyan elektrik yükleri iter ve zıt yükler çeker. Şekildeki etkileşim kuvvetlerinin yeri buna bağlıdır.

Zıt yükler göz önünde bulundurulursa, etkileşimlerinin kuvvetleri, çekimlerini gösteren birbirlerine doğru yönlendirilecektir.

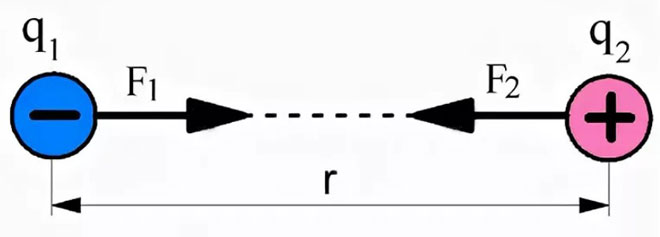
Farklı polariteye sahip iki nokta yükü için Coulomb kuvvetinin yönü.

Elektrostatik temel yasasının vektör biçimindeki formülü aşağıdaki gibi gösterilebilir:

$\vec F_1_2=\frac {1}{4\cdot \pi\cdot \varepsilon_0}\cdot \frac {q_1\cdot q_2}{r_1_2^3}\cdot \vec r_1_2$

$\vec F_1_2$ q2 yükünün yanından q1 nokta yüküne etkiyen kuvvet,

$\vec r_1_2$ q2 yükünü q1 yüküne bağlayan yarıçap vektörüdür

Ayrıca okuyun: Evde elektronik baskılı devre kartı nasıl yapılır?

$r=|\vec r_1_2|$

Önemli! Formülü vektör biçiminde yazdıktan sonra, işaretleri doğru yerleştirmek için iki noktalı elektrik yüklerinin etkileşen kuvvetlerinin eksene yansıtılması gerekecektir. Bu eylem bir formalitedir ve genellikle herhangi bir not olmaksızın zihinsel olarak gerçekleştirilir.

Coulomb yasasının pratikte uygulandığı yerler

Elektrostatiğin temel yasası, birçok alanda uygulamasını bulan Charles Coulomb'un en önemli keşfidir.

Ünlü fizikçinin eserleri, çeşitli cihazlar, cihazlar, aparatlar icat etme sürecinde kullanıldı. Örneğin, bir paratoner.

Bir paratoner yardımıyla, bir fırtına sırasında konut binaları ve binalar yıldırımdan korunur. Böylece, elektrikli ekipmanın koruma derecesi artar.

Paratoner şu prensibe göre çalışır: bir fırtına sırasında, yükselen ve bulutlara çekilen güçlü indüksiyon yükleri yavaş yavaş yerde birikmeye başlar. Bu durumda, yerde oldukça büyük bir elektrik alanı oluşur. Paratonerin yakınında, cihazın ucundan bir korona elektrik yükünün ateşlenmesi nedeniyle elektrik alanı güçlenir.

Ayrıca, yerde oluşan yük, Charles Coulomb yasasına göre olması gerektiği gibi, zıt işaretli bulutun yüküne çekilmeye başlar. Bundan sonra hava iyonlaşma sürecinden geçer ve elektrik alan gücü paratonerin ucuna yakın bir yerde azalır. Böylece binaya yıldırımın girme riski minimumdur.

Not! Paratonerin takıldığı binaya vurulursa yangın çıkmaz ve tüm enerji toprağa gider.

Coulomb yasasına dayanarak, günümüzde büyük talep gören "Parçacık Hızlandırıcı" adlı bir cihaz geliştirildi.

Bu cihazda, içine düşen parçacıkların enerjisini artıran güçlü bir elektrik alanı oluşturulur.

Coulomb yasasında kuvvetlerin yönü

Yukarıda bahsedildiği gibi, iki nokta elektrik yükünün etkileşen kuvvetlerinin yönü, polaritelerine bağlıdır. Şunlar. Aynı adı taşıyan suçlamalar itilecek ve karşıt suçlamalar cezbedecek.

Ayrıca okuyun: Kendi elinizle metal dedektörü nasıl yapılır, yeni başlayanlar için yardım

Coulomb kuvvetleri yarıçap vektörü olarak da adlandırılabilir, çünkü aralarına çizilen çizgi boyunca yönlendirilirler.

Bazı fiziksel problemlerde, bir nokta elektrik yükü olarak alınamayan karmaşık şekilli cisimler verilir, yani. boyutunu görmezden gelin. Bu durumda, incelenen cismin birkaç küçük parçaya bölünmesi ve her parçanın Coulomb yasası kullanılarak ayrı ayrı hesaplanması gerekir.

Bölme ile elde edilen kuvvet vektörleri cebir ve geometri kurallarına göre özetlenir. Sonuç, bu sorunun cevabı olacak olan ortaya çıkan kuvvettir. Bu çözme yöntemine genellikle üçgen yöntemi denir.

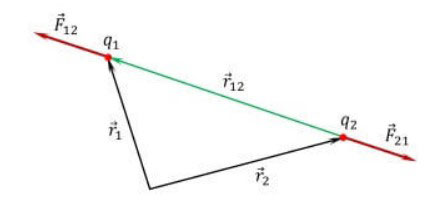
Coulomb kuvvet vektörlerinin yönü.

Yasanın keşfinin tarihi

Yukarıda ele alınan yasa ile iki nokta suçlamasının etkileşimleri ilk olarak 1785'te Charles Coulomb tarafından kanıtlandı. Fizikçi, çalışma prensibi makalede de sunulan burulma dengelerini kullanarak formüle edilen yasanın doğruluğunu kanıtlamayı başardı.

Coulomb ayrıca küresel bir kondansatörün içinde elektrik yükü olmadığını kanıtladı. Böylece, ele alınan cisimler arasındaki mesafeyi değiştirerek elektrostatik kuvvetlerin büyüklüğünün değiştirilebileceği ifadesine geldi.

Bu nedenle, Coulomb yasası hala en büyük keşiflerin çoğunun yapıldığı temel olarak elektrostatiklerin en önemli yasasıdır. Bu makale çerçevesinde, kanunun resmi üslubu sunulmuş ve kurucu unsurları ayrıntılı olarak anlatılmıştır.

Benzer makaleler: